Optimization and improvement of metaheuristic algorithms

Abstract

Addressing optimization problems is crucial in the study of a wide range of scientific and engineering issues. Therefore, new methods are emerging and being used to meet the new challenges of science and engineering. When it is difficult or impossible to find the optimal solution to a problem, such as NP-complete problems, a heuristic method is one way of quickly arriving at a viable solution. It is a strategy that provides feasible solutions in a reasonable amount of time and space but does not guarantee the best solution. A meta-heuristic is a generalized heuristic method that can be applied to a broader range of situations than the specific conditions of a particular problem.

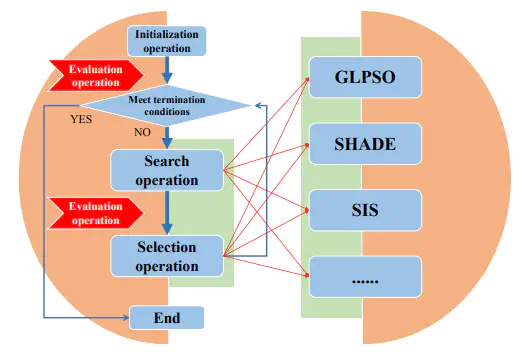
According to the well-known “No-Free-Lunch Theorem”, different meta-heuristic algorithms (MHAs) have corresponding advantages and disadvantages in addressing different optimization problems. Even so, much effort is still dedicated to creating algorithms that perform well on most problems. In recent decades, researchers appear to have concluded that maintaining a balance between exploitation and exploration is critical for improving MHAs’ performance. According to the latest definition of exploitation and exploration, the term “exploitation” refers to the idea of focusing the search process on promising areas of the solution space, whereas the ability of a search algorithm to discover a diverse array of solutions spread across different regions of the search space is emphasized by the term “exploration”. However, although new attempts to adjust the balance between exploitation and exploration are constantly being made, the issue of how to efficiently balance exploitation and exploration in algorithms remains a hot area of research.

Date
Nov 22, 2023 2:49 AM — 2:53 AM
Event
Group Research
Location
WeAI Research Group & University of Toyama

Researchers:

All members

Published Journals:

  1. Xu, Z., Yang, H., Li, J., Zhang, X., Lu, B., & Gao, S. (2021). Comparative study on single and multiple chaotic maps incorporated grey wolf optimization algorithms. IEEE Access, 9, 77416-77437.
  2. Xu, Z., Gao, S., Yang, H., & Lei, Z. (2021). SCJADE: Yet Another State‐of‐the‐Art Differential Evolution Algorithm. IEEJ Transactions on Electrical and Electronic Engineering, 16(4), 644-646.
  3. Yang, H., Gao, S., Wang, R. L., & Todo, Y. (2021). A ladder spherical evolution search algorithm. IEICE Transactions on Information and Systems, 104(3), 461-464.
  4. Yang, L., Gao, S., Yang, H., Cai, Z., Lei, Z., & Todo, Y. (2021). Adaptive chaotic spherical evolution algorithm. Memetic Computing, 13(3), 383-411.
  5. Li, J., Yang, L., Yi, J., Yang, H., Todo, Y., & Gao, S. (2022). A simple but efficient ranking-based differential evolution. IEICE Transactions on Information and Systems, 105(1), 189-192.
  6. Yang, H., Tao, S., Zhang, Z., Cai, Z., & Gao, S. (2022). Spatial information sampling: another feedback mechanism of realising adaptive parameter control in meta-heuristic algorithms. International Journal of Bio-Inspired Computation, 19(1), 48-58.
  7. Li, X., Wang, K., Yang, H., Tao, S., Feng, S., & Gao, S. (2022). PAIDDE: A permutation-archive information directed differential evolution algorithm. IEEE Access, 10, 50384-50402.
  8. Zhang, B., Yang, H., Zheng, T., Wang, R. L., & Gao, S. (2023). A non-revisiting equilibrium optimizer algorithm. IEICE TRANSACTIONS on Information and Systems, 106(3), 365-373.
  9. Li, H., Yang, H., Zhang, B., Zhang, H., & Gao, S. (2023). Swarm Exploration Mechanism-Based Distributed Water Wave Optimization. International Journal of Computational Intelligence Systems, 16(1), 1-26.
Haichuan Yang 楊海川
Haichuan Yang 楊海川
assistant professor

My research interests include meta-heuristic algorithms, artificial neuron model and complex systems.